Tabla de contenido:
Video: ¿Cómo hallas la proporción de una desviación estándar?
2024 Autor: Miles Stephen | [email protected]. Última modificación: 2023-12-15 23:35
La regla 68-95-99.7 establece que el 68% de a Los valores de la distribución normal están dentro una desviación estándar de la media. 95% están dentro de dos desviaciones estandar y el 99,7% están dentro de los tres desviaciones estandar . Eso significa que el proporción de valores dentro una desviación estándar es 68/100 = 17/25.
Entonces, ¿cómo hallas el porcentaje de una desviación estándar?
La regla empírica o la regla del 68-95-99,7% puede darnos un buen punto de partida. Esta regla nos dice que alrededor del 68% de los datos caerán dentro de uno Desviación Estándar de la media; alrededor del 95% caerá dentro de dos desviaciones estandar de themean; y el 99,7% caerá dentro de Tres desviaciones estandar de la media.
Además, ¿qué porcentaje de los datos está dentro de 2 desviaciones estándar de la media? Para datos con una distribución simétrica, aproximadamente 68,3 por ciento de los valores caerán dentro de uno Desviación Estándar desde el significar , aproximadamente 95,4 por ciento caerá dentro de 2 desviaciones estándar desde el significar y aproximadamente 99,7 por ciento caerá dentro de 3 desviaciones estandar desde el significar.
¿Cómo se encuentra la desviación estándar de un tamaño de muestra?
Primero, repasemos los pasos para calcular la desviación estándar de la muestra:
- Calcule la media (promedio simple de los números).
- Para cada número: reste la media.
- Sume todos los resultados al cuadrado.
- Divida esta suma por uno menos que el número de puntos de datos (N-1).
¿Cuál es la fórmula de la desviación estándar?
los Desviación Estándar es dado por el fórmula : s significa ' Desviación Estándar '. Ahora, reste la media individualmente de cada uno de los números dados y eleve al cuadrado el resultado. Esto es equivalente al paso (x -) ².
Recomendado:
¿Cómo se calcula la desviación estándar de PMP?
La fórmula utilizada en el PMBOK para la desviación estándar es simple. Es solo (P-O) / 6. Esa es la estimación de la actividad pesimista menos la estimación de la actividad optimista dividida por seis. El problema es que esta forma de ninguna manera produce una medida de desviación estándar
¿Cómo se calcula la desviación estándar en SPC?
Calcular la desviación estándar Calcular el promedio del proceso μ Restar el promedio del proceso de cada valor de datos medidos (los valores X i) Cuadrar cada una de las desviaciones calculadas en el paso 2. Sume todas las desviaciones cuadradas calculadas en el paso 3. Divida el resultado de paso 4 por el tamaño de la muestra
¿Cómo encuentra la desviación estándar y la media en Excel?
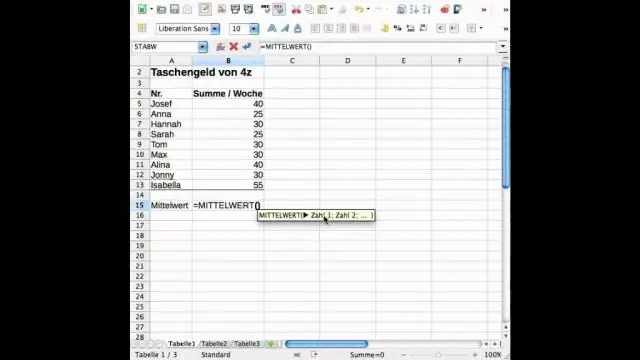
La desviación estándar es una medida de cuánta varianza hay en un conjunto de números en comparación con el promedio (media) de los números. Para calcular la desviación estándar en Excel, puede utilizar una de las dos funciones principales, según el conjunto de datos. Si los datos representan a toda la población, puede utilizar STDEV. Función
¿Cómo encuentra la desviación estándar de la variabilidad?
Para calcular la desviación estándar, sume todos los puntos de datos y divídalos por el número de puntos de datos, calcule la varianza para cada punto de datos y luego encuentre la raíz cuadrada de la varianza
¿Cuál es el símbolo de la desviación estándar en una TI 84 Plus?
El símbolo Sx representa la desviación estándar de la muestra y el símbolo σ significa población desviación estándar