
Tabla de contenido:
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:35.
- Última modificación 2025-01-22 16:57.
• Descripciones verbales : a descripción verbal de un conjunto utiliza una oración en inglés para enunciar una regla que nos permite determinar la clase de objetos que se están discutiendo y determinar para cualquier objeto en particular si está o no en el conjunto.
En consecuencia, ¿qué es la descripción verbal?
Definición. Descripción verbal utiliza un lenguaje no visual para transmitir el mundo visual. Puede navegar durante una visita a través de un museo, orientar al oyente hacia una obra de arte o proporcionar acceso a los aspectos visuales de una actuación.
Además, ¿cómo describe un conjunto en matemáticas? En matemáticas , a colocar es una colección de objetos distintos bien definidos, considerados como un objeto por derecho propio. Por ejemplo, los números 2, 4 y 6 son objetos distintos cuando se consideran por separado, pero cuando se consideran colectivamente forman un solo objeto. colocar de tamaño tres, escrito {2, 4, 6}.
Simplemente, ¿cómo se describe una función verbalmente?
Conclusiones clave
- Una función se puede representar verbalmente. Por ejemplo, la circunferencia de un cuadrado es cuatro veces uno de sus lados.
- Una función se puede representar algebraicamente. Por ejemplo, 3x + 63 x + 6.
- Una función se puede representar numéricamente.
- Una función se puede representar gráficamente.
¿Qué es una relación en matemáticas?
A relación es un relación entre conjuntos de valores. En Matemáticas , los relación está entre los valores xy los valores y de pares ordenados. El conjunto de todos los valores de x se llama dominio, y el conjunto de todos los valores de y se llama rango. Los corchetes se utilizan para mostrar que los valores forman un conjunto.
Recomendado:
¿Qué es una representación verbal en matemáticas?
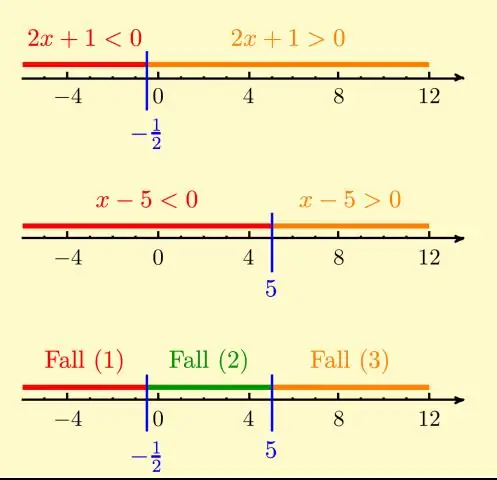
Un modelo verbal es una ecuación de palabras que representa una situación real. En otras palabras, usa palabras para describir ideas y símbolos matemáticos para relacionar las palabras. No se utilizan números en los modelos verbales, pero los símbolos matemáticos son importantes y el modelo debe ser verdadero
¿Cuál es la descripción de un rectángulo?

En la geometría del plano euclidiano, un rectángulo es aquadrilátero con cuatro ángulos rectos. También se puede definir como un cuadrilátero cuadrilátero, ya que equiangular significa que todos sus ángulos son iguales (360 ° / 4 = 90 °). También se puede definir como un paralelogramo que contiene un ángulo recto
¿Qué tipo de matemáticas son las matemáticas del consumidor?
Un curso de matemáticas para consumidores de EE. UU. Puede incluir una revisión de aritmética elemental, incluidas fracciones, decimales y porcentajes. El álgebra elemental también se incluye a menudo, en el contexto de la resolución de problemas empresariales prácticos
¿Cómo el contraste en la descripción física y de comportamiento de Pearl la desarrolla como personaje?

¿Cómo el contraste en la descripción física y de comportamiento de Pearl la desarrolla como personaje? Pearl es bella por fuera pero de comportamiento salvaje. Esto la desarrolla porque los puritanos aprueban una belleza tan fuerte, pero desdeñan a Pearl por su fuerte personalidad
¿Cuál es la mejor descripción de lo que es una nebulosa planetaria?

Una nebulosa planetaria es un objeto astronómico que consiste en una capa brillante de gas y plasma formada por ciertos tipos de estrellas al final de sus vidas. De hecho, no están relacionados con los planetas; el nombre se origina en una supuesta similitud en apariencia con planetas gigantes
