Video: ¿Cuál es la fórmula de distribución de probabilidad?
2024 Autor: Miles Stephen | [email protected]. Última modificación: 2023-12-15 23:35
Para calcular esto, multiplicamos cada valor posible de la variable por su probabilidad , luego agregue los resultados. Σ (xI × P (xI)) = {x1 × P (x1)} + {x2 × P (x2)} + {x3 × P (x3)} + E (X) también se llama la media de la Distribución de probabilidad.
Simplemente, ¿cómo se encuentra la distribución de probabilidad?
Probabilidad . Probabilidad es la probabilidad de que ocurra un evento y es calculado dividiendo el número de resultados favorables por el número total de resultados posibles. El ejemplo más simple es el lanzamiento de una moneda. Cuando lanza una moneda, solo hay dos resultados posibles, el resultado es cara o cruz.
Además, ¿qué es una función de distribución en probabilidad? los función de distribución , también llamado acumulativo función de distribución (CDF) o frecuencia acumulada función , describe el probabilidad que una variable adquiere un valor menor o igual que un número. los función de distribución a veces también se denota. (Evans y col. 2000, pág. 6).
En este sentido, ¿cuál es la fórmula de probabilidad?
Fórmula de probabilidad es la relación entre el número de resultados favorables y el número total de resultados posibles. Mide la probabilidad de un evento de la siguiente manera: - Si P (A)> P (B), entonces es más probable que ocurra el evento A que el evento B. - Si P (A) = P (B), entonces los eventos A y B es igualmente probable que ocurran.
¿Cuál es un ejemplo de distribución de probabilidad?
los Distribución de probabilidad de una variable aleatoria discreta siempre se puede representar mediante una tabla. Para ejemplo , suponga que lanza una moneda dos veces. Para ejemplo , los probabilidad de obtener 1 cara o menos [P (X <1)] es P (X = 0) + P (X = 1), que es igual a 0,25 + 0,50 o 0,75.
Recomendado:
¿Qué es la curva de distribución de probabilidad radial?
La curva de distribución radial da una idea de la densidad de electrones a una distancia radial del núcleo. El valor de 4 π r2ψ2 (función de densidad de probabilidad radial) se vuelve cero en un punto nodal, también conocido como nodo radial. Donde n = número cuántico principal yl = número cuántico azimutal
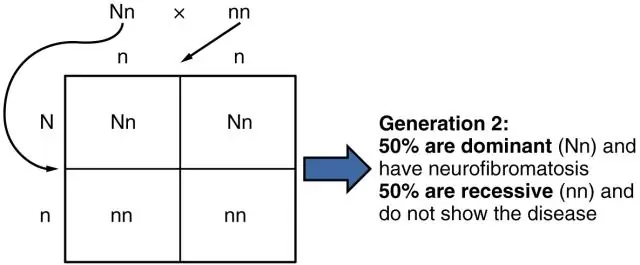
¿Cuál es la probabilidad de que su hijo tenga la enfermedad?
En general, si uno de los padres no es portador, la probabilidad de que un hijo sea portador es: ½ veces (la probabilidad de que el otro padre sea portador). Es decir, multiplicamos la probabilidad de transmitir un alelo de la enfermedad, ½, por la probabilidad de que el padre, de hecho, sea portador del alelo de la enfermedad
¿Cuál es la media de la distribución de chi cuadrado?
La distribución de Chi cuadrado es la distribución de la suma de las desviaciones normales estándar al cuadrado. Los grados de libertad de la distribución son iguales al número de desviaciones normales estándar que se suman. La media de una distribución de Chi cuadrado son sus grados de libertad
¿Cuál es la diferencia entre probabilidad condicional y probabilidad conjunta?
En términos generales, la probabilidad conjunta es la probabilidad de que dos cosas * sucedan juntas: por ejemplo, la probabilidad de que lave mi coche y llueva. La probabilidad condicional es la probabilidad de que suceda una cosa, dado que sucede la otra: por ejemplo, la probabilidad de que, dado que lavo mi auto, llueva
¿Cuál es el propósito de una distribución de frecuencia?
Una tabla de distribución de frecuencia es un gráfico que resume los valores y su frecuencia. Es una forma útil de organizar los datos si tiene una lista de números que representan la frecuencia de un resultado determinado en una muestra. Una tabla de distribución de frecuencia tiene dos columnas