Tabla de contenido:
Video: ¿Cómo se encuentra el ángulo de un sector en un gráfico circular?
2024 Autor: Miles Stephen | [email protected]. Última modificación: 2023-12-15 23:35
1 respuesta
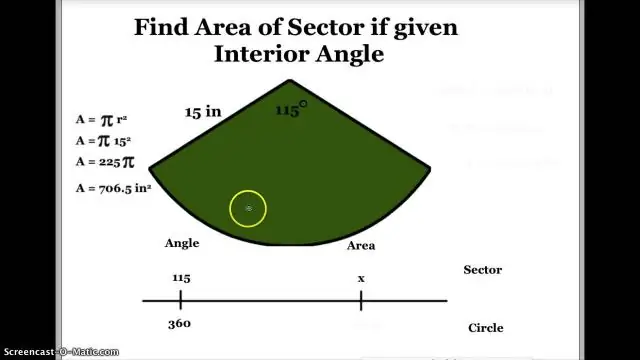
- En cualquier sector , hay 3 partes a considerar:
- La longitud del arco es una fracción de la circunferencia. sector el área es una fracción del área total. los sector es una fracción de 360 °
- Si el sector es el 20% del Gráfico circular , cada una de estas partes es el 20% del total.
- 20%×360°
- 20100×360=72°
De esta manera, ¿cómo se encuentra el grado de un sector de un círculo?
Explicación: Si el ángulo central mide 60 grados , divide el total de 360 grados en el circulo por 60. Multiplique esto por la medida del arco correspondiente a encontrar la circunferencia total de la circulo . Usa la circunferencia para encontrar theradius, luego use el radio para encontrar la zona.
Posteriormente, la pregunta es, ¿qué es un ángulo central en un gráfico circular? en un Gráfico circular , las diversas observaciones o componentes están representados por los sectores de un círculo y el círculo completo representa la suma de los valores de todos los componentes. ángulo central para un componente viene dado por: Centralangle para un componente = Valor del componente Suma de los valores de todos los componentes × 360 °
Asimismo, ¿cómo se encuentra el grado de un porcentaje?
Un círculo tiene 360 grados , por lo que si desea expresar un ángulo en términos de porcentaje , simplemente divida la medida del ángulo (en grados ) por 360 y multiplicar por 100. A la inversa, dividir el porcentaje por 100 y multiplicar por 360.
¿Cuál es la fórmula para encontrar el ángulo central?
Fórmula para S = rθ La siguiente imagen ilustra la relación entre el radio y la ángulo central en radianes. fórmula es S = rθ donde s representa la longitud de arco, S = rθ representa la ángulo central en radianes y r es la longitud del radio.
Recomendado:
¿Cómo hallas el ángulo central dados el área y el radio de un sector?
Determinación del ángulo central desde el área del sector (πr2) × (ángulo central en grados ÷ 360 grados) = área del sector. Si el ángulo central se mide en radianes, la fórmula en cambio se convierte en: área del sector = r2 × (ángulo central en radianes ÷ 2). (θ ÷ 360 grados) × πr2. (52,3 ÷ 100π) × 360. (52,3 ÷ 314) × 360
¿Cómo se encuentra la longitud del arco y el área del sector?
Un ángulo central que está subtendido por un arco mayor tiene una medida mayor a 180 °. La fórmula de la longitud del arco se usa para encontrar la longitud de un arco de un círculo; l = r θ l = r θ, donde θ está en radianes. El área del sector se encuentra A = 12 θ r2 A = 1 2 θ r 2, donde θ está en radianes
¿Cómo se encuentra la distancia desde un gráfico de tiempo de posición?
VIDEO También la pregunta es, ¿es un gráfico de tiempo de posición lo mismo que un gráfico de tiempo de distancia? Hasta donde yo sé, un posición - tiempo y desplazamiento tiempo son exactamente los mismo cosa, aunque podría estar usando una definición ligeramente diferente.
¿Cómo se encuentra la tensión en el movimiento circular?
Suponiendo que el movimiento circular es llevado por una cuerda y una masa unida a uno de sus extremos, entonces la tensión en la cuerda puede equipararse a la fuerza centrífuga. v = velocidad del objeto (tangencialmente). r = longitud de la cuerda
¿Cómo se encuentra la velocidad promedio en un gráfico de velocidad en función del tiempo?
El área bajo la curva de velocidad / tiempo es el desplazamiento total. Si divide eso por el cambio en el tiempo, obtendrá la velocidad promedio. La velocidad es la forma vectorial de la velocidad. Si la velocidad siempre es no negativa, entonces la velocidad promedio y la velocidad promedio son iguales