Video: ¿Qué es la Directrix en una parábola?
2024 Autor: Miles Stephen | [email protected]. Última modificación: 2023-12-15 23:35
Directora . A parábola es un conjunto de todos los puntos en un plano que están a la misma distancia de un punto y una línea dados. El punto se llama el foco de la parábola , y la línea se llama directora . los directora es perpendicular al eje de simetría de un parábola y no toca el parábola.
Además, ¿cómo se encuentra la Directriz de una parábola?
La forma estándar es (x - h)2 = 4p (y - k), donde el foco es (h, k + p) y el directora es y = k - p. Si el parábola se gira para que su vértice sea (h, k) y su eje de simetría sea paralelo al eje x, tiene una ecuación de (y - k)2 = 4p (x - h), donde el foco es (h + p, k) y el directora es x = h - p.
Además, ¿cómo se encuentra la forma de vértice de una parábola? f (x) = a (x - h)2 + k, donde (h, k) es el vértice de El parábola . FYI: Diferentes libros de texto tienen diferentes interpretaciones de la referencia "estándar formulario "de una función cuadrática. Algunos dicen que f (x) = ax2 + bx + c es "estándar formulario ", mientras que otros dicen que f (x) = a (x - h)2 + k es "estándar formulario ".
De manera similar, uno puede preguntarse, ¿cuál es la directriz de una hipérbola?
En el caso de un hipérbola , a directora es una línea recta donde la distancia desde cada punto en el hipérbola a uno de sus dos focos es multiplicada por la distancia perpendicular desde al directora , donde es una constante mayor que. Tenga en cuenta que hipérbolas tienen dos focos y dos directrices, una para cada foco.
¿Cómo hallas la Directriz de una ecuación?
La forma estándar es (x - h)2 = 4p (y - k), donde el foco es (h, k + p) y el directora es y = k - p. Si la parábola se gira de modo que su vértice es (h, k) y su eje de simetría es paralelo al eje x, tiene un ecuación de (y - k)2 = 4p (x - h), donde el foco es (h + p, k) y el directora es x = h - p.
Recomendado:
¿Qué tipo de ecuación es una parábola?
La forma estándar es (x - h) 2 = 4p (y - k), donde el foco es (h, k + p) y la directriz es y = k - p. Si la parábola se gira de modo que su vértice es (h, k) y su eje de simetría es paralelo al eje x, tiene una ecuación de (y - k) 2 = 4p (x - h), donde el foco es (h + p, k) y la directriz es x = h - p
¿Es el Arco de San Luis una parábola?
Este artículo ha demostrado que Gateway Arch no es una parábola. Más bien, tiene la forma de una catenaria aplanada (o ponderada), que es la forma que vemos si colgamos una cadena delgada en el medio entre dos puntos fijos
¿Cuál es el punto máximo o mínimo de una parábola?
Las parábolas verticales brindan una información importante: cuando la parábola se abre, el vértice es el punto más bajo de la gráfica, llamado mínimo o min. Cuando la parábola se abre hacia abajo, el vértice es el punto más alto del gráfico, llamado máximo o máximo
¿Cómo grafica una cónica de una parábola?
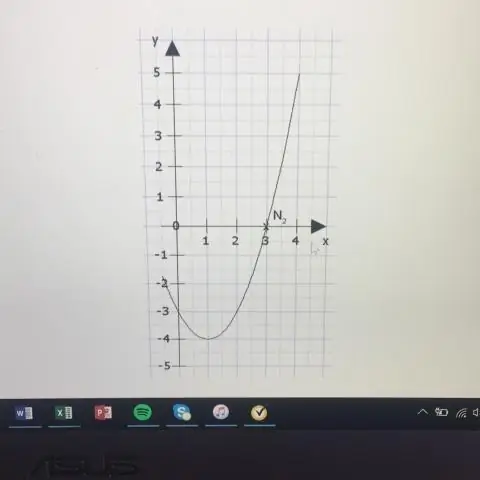
La directriz es la recta y = k - p. El eje es la recta x = h. Si p> 0, la parábola se abre hacia arriba, y si p <0, la parábola se abre hacia abajo. Si una parábola tiene un eje horizontal, la forma estándar de la ecuación de la parábola es la siguiente: (y - k) 2 = 4p (x - h), donde p ≠ 0
¿Cómo se hace una sección cónica de una parábola?
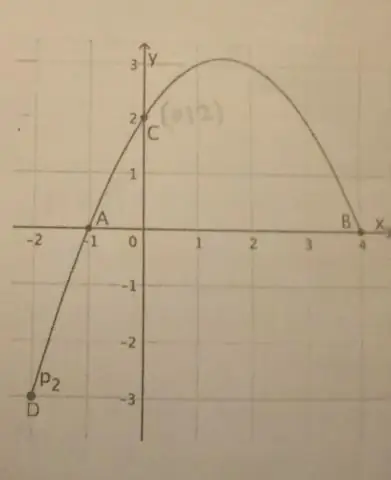
Si una parábola tiene un eje vertical, la forma estándar de la ecuación de la parábola es la siguiente: (x - h) 2 = 4p (y - k), donde p ≠ 0. El vértice de esta parábola está en (h, k). El foco está en (h, k + p). La directriz es la recta y = k - p