Tabla de contenido:
Video: ¿Cómo se calcula la distribución de chi cuadrado?
2024 Autor: Miles Stephen | [email protected]. Última modificación: 2023-12-15 23:35
Distribución chi-cuadrado
- La media de la distribución es igual al número de grados de libertad: μ = v.
- La varianza es igual a dos veces el número de grados de libertad: σ2 = 2 * v.
- Cuando los grados de libertad son mayores o iguales a 2, el valor máximo de Y ocurre cuando Χ2 = v - 2.
Con respecto a esto, ¿qué te dice una distribución de chi cuadrado?
los Chi - cuadrado La prueba está destinada a probar la probabilidad de que un distribución se debe al azar. También se denomina estadística de "bondad de ajuste", porque mide qué tan bien distribución de datos encaja con el distribución que se espera si las variables son independientes.
¿Cómo se ve una distribución de chi cuadrado? La media de un Distribución de Chi cuadrado son sus grados de libertad. Distribuciones de Chi cuadrado están positivamente sesgados, y el grado de sesgo disminuye al aumentar los grados de libertad. A medida que aumentan los grados de libertad, la Distribución de Chi cuadrado se acerca a un normal distribución.
Además, ¿cómo se usa una tabla de distribución de chi cuadrado?
En resumen, estos son los pasos que debe seguir al usar la tabla de chi-cuadrado para encontrar un valor de chi-cuadrado:
- Encuentre la fila que corresponda a los grados de libertad relevantes, r.
- Encuentra la columna encabezada por la probabilidad de interés.
- Determine el valor de chi-cuadrado donde se cruzan la fila r y la columna de probabilidad.
¿Cómo calcula el valor esperado?
En estadística y análisis de probabilidad, el valor esperado es calculado multiplicando cada uno de los posibles resultados por la probabilidad de que ocurra cada resultado y luego sumando todos esos valores . Por calcular los valores esperados , los inversores pueden elegir el escenario con más probabilidades de obtener el resultado deseado.
Recomendado:
¿De dónde proviene la distribución chi cuadrado?
La distribución de chi-cuadrado se obtiene como la suma de los cuadrados de k variables aleatorias gaussianas independientes, de media cero y de varianza unitaria. Las generalizaciones de esta distribución se pueden obtener sumando los cuadrados de otros tipos de variables aleatorias gaussianas
¿Es pecado al cuadrado x igual a sin x al cuadrado?
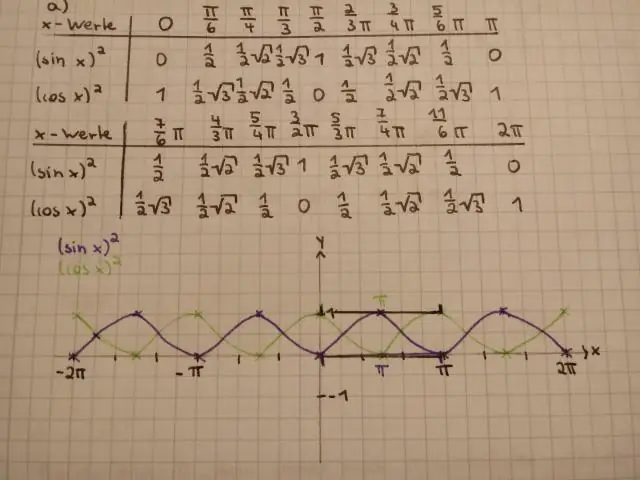
Sí lo es. sin ^ 2x es el mismo assinx ^ 2 porque en ambos casos el '^ 2' se relaciona solo con la x
¿Cuál es la media de la distribución de chi cuadrado?
La distribución de Chi cuadrado es la distribución de la suma de las desviaciones normales estándar al cuadrado. Los grados de libertad de la distribución son iguales al número de desviaciones normales estándar que se suman. La media de una distribución de Chi cuadrado son sus grados de libertad
¿Cómo se usa el chi cuadrado en genética?
El análisis genético a menudo requiere la interpretación de números en varias clases fenotípicas. En tales casos, se utiliza un procedimiento estadístico llamado prueba de χ 2 (chi-cuadrado) para ayudar a tomar la decisión de mantener o rechazar la hipótesis
¿Cómo encuentras la razón esperada en una prueba de chi cuadrado?
Para calcular 2, primero determine el número esperado en cada categoría. Si la proporción es 3: 1 y el número total de individuos observados es 880, entonces los valores numéricos esperados deben ser 660 verdes y 220 amarillos. Chi-cuadrado requiere que use valores numéricos, no porcentajes o razones